Material Requirements Planning - Calculations
MRP (material requirements planning) is basically is a demand explosion concept without any planning functionality, as will be shown below. The data required for these calculations are 1) bill-of-material structure, 2) external demands for end products 3) starting inventory levels (including planned order arrivals) and 4) planned lead times.
The MRP calculations are as follows:
a) Sort items according to their low level code.
b) Consider each item in sequence and perform the following steps:
- Get external demand (from the master production schedule), sif any
- Compute derived demands
- Get available inventory (from the inventory records)
- Compute net demand
- Compute lot sizes (usually with the a heuristic for the single level dynamic lot sizing problem)
- Offset lots according to the planned lead time and fix production dates
Here is a numerical example:
Consider the following Bill-of-Material (BOM) structure with seven items:
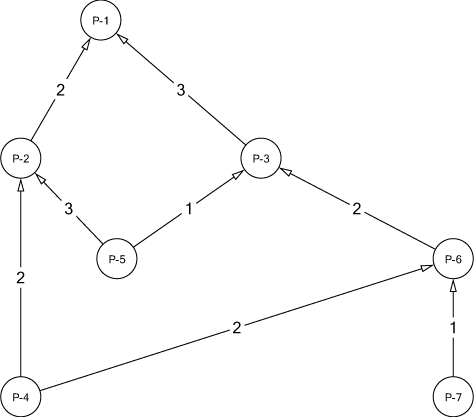
There is a demand of 35 units in period 8 for the end product. The initial inventory on hand for each item is given in the following table:
Product |
P-1 |
P-2 |
P-3 |
P-4 |
P-5 |
P-6 |
P-7 |
|---|---|---|---|---|---|---|---|
Inventory |
10 |
15 |
20 |
10 |
10 |
10 |
30 |
For each item 5 unit of safety stock are required. The remaining data are shown in the following table:
Product |
Setup Costs |
Holding Costs |
Setup Times |
Processing Times |
Resource |
Lead Time |
|---|---|---|---|---|---|---|
P-1 |
100 |
4 |
10 |
1 |
1 |
1 |
P-2 |
100 |
3 |
10 |
1 |
1 |
2 |
P-3 |
100 |
2 |
10 |
1 |
2 |
1 |
P-4 |
100 |
1 |
10 |
1 |
2 |
1 |
P-5 |
100 |
1 |
10 |
1 |
3 |
2 |
P-6 |
100 |
1 |
10 |
1 |
3 |
3 |
P-7 |
100 |
1 |
10 |
1 |
4 |
2 |
Note that setup times, processing times and the associated resources are not used in the MRP calculations. They are presented here as we will show that the MRP calculations may results in infeasible workloads for the resources.
The lot sizes for each item are computed with the Silver-Meal heuristic. Here future demands are added to the current lot as long as the average costs per period are reduced. The Silver-Meal criterion is:
cτt=s+h⋅∑l=τt(l-τ)⋅dlt-τ+1τ≤t
where τ = production period, s = setup costs, h = holdings costs, dl = demand of period l, t = last period currently covered by the lot produced in periode τ.
For the above example, the results of the MRP calculations are given in the following table:
Period |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|---|---|---|---|---|---|---|---|---|
| Level u= 0; product k=P-1; lead time z= 1; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
- |
- |
- |
- |
- |
35 |
| Inventory on hand | 10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
| Net requirements | - |
- |
- |
- |
- |
- |
- |
30 |
| Lot sizes | - |
- |
- |
- |
- |
- |
30 |
- |
| Level u= 1; product k=P-2; lead time z= 2; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
- |
- |
- |
- |
60 |
- |
| Inventory on hand | 15 |
15 |
15 |
15 |
15 |
15 |
15 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 10 |
10 |
10 |
10 |
10 |
10 |
10 |
- |
| Net requirements | - |
- |
- |
- |
- |
- |
50 |
- |
| Lot sizes | - |
- |
- |
- |
50 |
- |
- |
- |
| Level u= 1; product k=P-3; lead time z= 1; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
- |
- |
- |
- |
90 |
- |
| Inventory on hand | 20 |
20 |
20 |
20 |
20 |
20 |
20 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 15 |
15 |
15 |
15 |
15 |
15 |
15 |
- |
| Net requirements | - |
- |
- |
- |
- |
- |
75 |
- |
| Lot sizes | - |
- |
- |
- |
- |
75 |
- |
- |
| Level u= 2; product k=P-5; lead time z= 2; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
- |
- |
150 |
75 |
- |
- |
| Inventory on hand | 10 |
10 |
10 |
10 |
10 |
5 |
5 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 5 |
5 |
5 |
5 |
5 |
- |
- |
- |
| Net requirements | - |
- |
- |
- |
145 |
75 |
- |
- |
| Lot sizes | - |
- |
220 |
- |
- |
- |
- |
- |
| Level u= 2; product k=P-6; lead time z= 3; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
- |
- |
- |
150 |
- |
- |
| Inventory on hand | 10 |
10 |
10 |
10 |
10 |
10 |
5 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 5 |
5 |
5 |
5 |
5 |
5 |
- |
- |
| Net requirements | - |
- |
- |
- |
- |
145 |
- |
- |
| Lot sizes | - |
- |
145 |
- |
- |
- |
- |
- |
| Level u= 3; product k=P-4; lead time z= 1; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
290 |
- |
100 |
- |
- |
- |
| Inventory on hand | 10 |
10 |
10 |
5 |
5 |
5 |
5 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 5 |
5 |
5 |
- |
- |
- |
- |
- |
| Net requirements | - |
- |
285 |
- |
100 |
- |
- |
- |
| Lot sizes | - |
385 |
- |
- |
- |
- |
- |
- |
| Level u= 3; product k=P-7; lead time z= 2; safety stock = 5 | ||||||||
| Gross requirements | - |
- |
145 |
- |
- |
- |
- |
- |
| Inventory on hand | 30 |
30 |
30 |
5 |
5 |
5 |
5 |
5 |
| Planned receipts | - |
- |
- |
- |
- |
- |
- |
- |
| Available inventory | 25 |
25 |
25 |
- |
- |
- |
- |
- |
| Net requirements | - |
- |
120 |
- |
- |
- |
- |
- |
| Lot sizes | 120 |
- |
- |
- |
- |
- |
- |
- |
Here is the production plan:
Period |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|---|---|---|---|---|---|---|---|---|
P-1 |
0 |
0 |
0 |
0 |
0 |
0 |
30 |
0 |
P-2 |
0 |
0 |
0 |
0 |
50 |
0 |
0 |
0 |
P-3 |
0 |
0 |
0 |
0 |
0 |
75 |
0 |
0 |
P-4 |
0 |
385 |
0 |
0 |
0 |
0 |
0 |
0 |
P-5 |
0 |
0 |
220 |
0 |
0 |
0 |
0 |
0 |
P-6 |
0 |
0 |
145 |
0 |
0 |
0 |
0 |
0 |
P-7 |
120 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Based on the above setup and processing time data, which are completely neglected during the MRP calculations, the following workloads of the resources result:
Period |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|---|---|---|---|---|---|---|---|---|
Ressource 1 |
0 |
0 |
0 |
0 |
60 |
0 |
40 |
0 |
Ressource 2 |
0 |
395 |
0 |
0 |
0 |
85 |
0 |
0 |
Ressource 3 |
0 |
0 |
385 |
0 |
0 |
0 |
0 |
0 |
Ressource 4 |
130 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Note that the workloads differ extremely among the periods. In industrial practice a production plan computed with the above methods usually will be infeasible.